Architecture
Cairo is a STARK-friendly Von Neumann architecture capable of generating validity proofs for arbitrary computations. Being STARK-friendly means that Cairo's design is optimized for the STARK proof system, while remaining compatible with other proof system backends. It implements a Turing-complete process virtual machine.
Cairo consists of three main components:
- The Cairo compiler
- The Cairo Virtual Machine (CairoVM)
- The Cairo prover and verifier
The Cairo compiler transforms Cairo source code into Cairo bytecode (encoded instructions and metadata). The compiler's output is commonly referred to as the compilation artifacts.
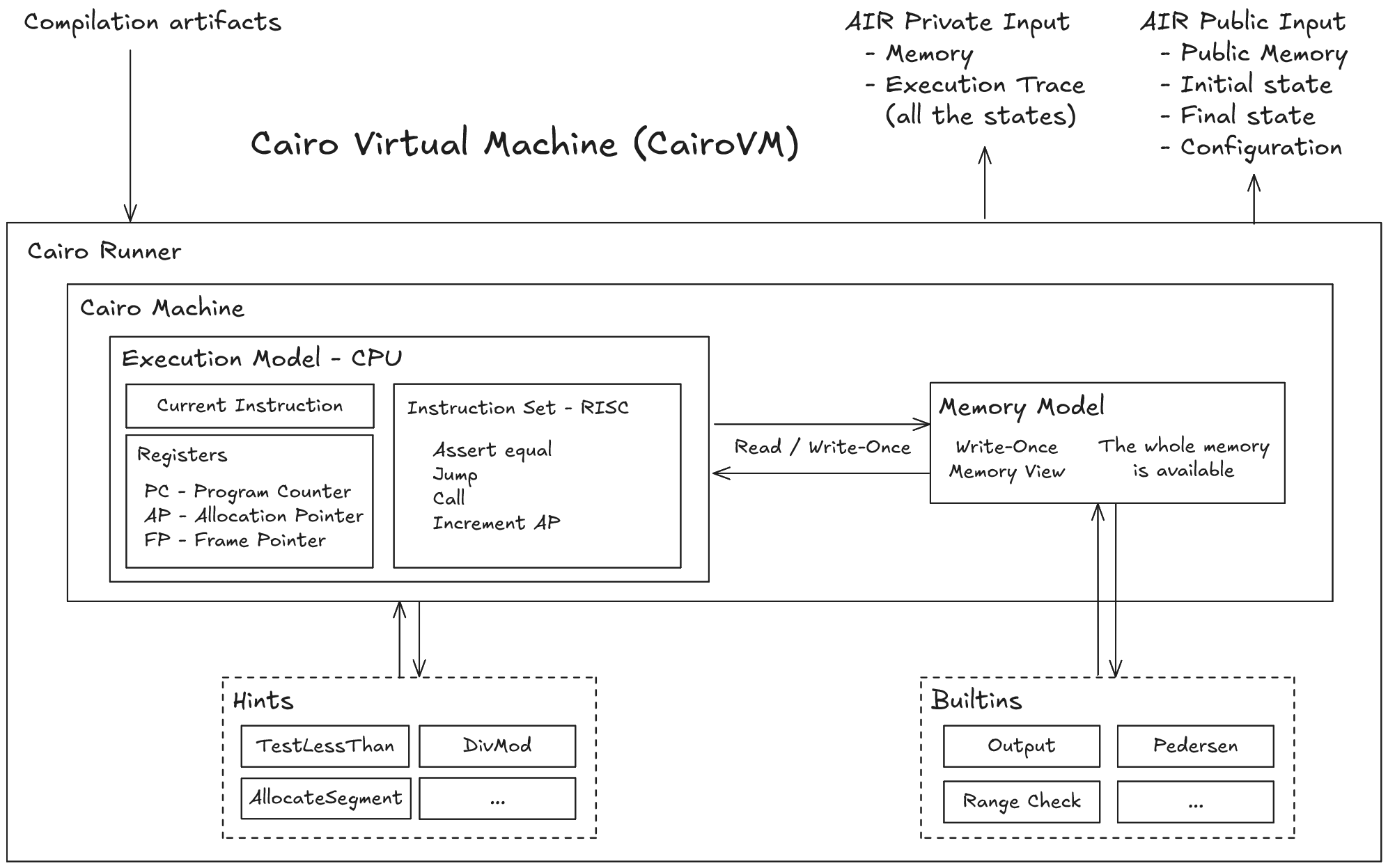
The CairoVM implements the theoretical Cairo machine, processing the compilation artifacts and executing the instructions to produce two key outputs required for proof generation and verification: the AIR (Arithmetic Intermediate Representation) private input (witness) and AIR public input:
- The AIR private input comprises the execution trace (or simply "trace") and the memory.
- The AIR public input includes the initial and final states (first and last entries of the trace), the public memory (a subset of the memory), and configuration data (e.g., layout) of the execution.
The prover takes the AIR's private and public inputs to generate a proof of the corresponding program execution. The verifier can then verify the proof's correctness asynchronously, given the proof and the AIR public input.
What are AIRs, though?
Arithmetic Intermediate Representation - AIR
AIR stands for Arithmetic Intermediate Representation, which is an arithmetization technique. Arithmetization is the foundation of every proof system: STARK uses AIRs, while other proof systems might rely on different techniques (e.g., R1CS, PLONKish arithmetization). It allows converting a computational statement into a set of polynomial equations. These polynomial equations then represent the constraints of your system: if they all hold while following the proof system protocol, then the proof is valid; otherwise, it's invalid.
At its core, Cairo is a set of AIRs that represent a Turing-complete machine for the Cairo ISA: the Cairo machine. This enables proving any statement (i.e., arbitrary code) through the Cairo machine.
The Cairo machine abstracts away the need to write AIRs for the program you would like to prove, and Cairo, as a language, provides a human-readable interface to use the Cairo machine.
Each component of the Cairo machine has its corresponding AIR: the CPU, the Memory, the Builtins...
Good AIRs are critical to the performance of proof generation and verification. While there can be many ways to express a computational statement into polynomials, not all are equally efficient. Writing optimal AIRs is a strong factor of performance.
We won't go any further on AIRs here, but it's good to know that the CairoVM's purpose is to provide the required inputs to the Cairo prover for it to generate proof of the given Cairo program. In a nutshell, the Cairo prover and verifier job is to verify that the constraints defined by the Cairo AIR holds for the CairoVM outputs.
Cairo Machine
The Cairo machine is the theoretical model that defines the Von Neumann architecture to prove arbitrary computation.
The machine is defined by two core models:
- CPU, or Execution model - The Instruction Set Architecture (ISA)
- Memory model - Non-deterministic Read-only Memory
The Execution model specifies the ISA through three key components:
- The instruction set
- The registers (
pc,ap,fp) - The state transition algorithm
Unlike general-purpose ISAs such as RISC-V, Cairo implements its own ISA specifically optimized for proof generation and verification—a custom zero-knowledge ISA (ZK-ISA). The Memory model defines how the CPU interacts with the memory. Following Von Neumann architecture principles, a single memory stores both program and instruction data.
The Cairo machine exists in two versions:
- The deterministic machine (used by the prover)
- The non-deterministic machine (used by the verifier)
Why are there two versions of the Cairo machine, one for the prover and one for the verifier?
Deterministic and Non-deterministic Cairo Machine
The deterministic machine takes a trace (a sequence of states) and the whole memory
(a memory function), and verifies that the transition between two consecutive states is valid.
It returns accept if all state transitions are valid and reject otherwise.
This machine does not perform any computation, it only asserts the validity of a trace
and its memory.
The non-deterministic machine relies on the deterministic one: it only takes the initial
state, the final state, and a partial memory function (i.e. the public memory)
and returns accept if there exists a sequence of states (a trace)
with the same initial and final states and a memory function that extends the partial memory
(a whole memory that includes the public-memory) which is accepted by the deterministic machine.
The deterministic machine allows the prover to generate a proof, while the non-deterministic machine allows the verifier to verify the proof succinctly in a zero-knowledge way (some data can be kept private from the verifier).
The CairoVM is the implementation of this theoretical machine, including some functionalities to benefit from its design (builtins & hints). Among the various implementations of the CairoVM, what we call the Cairo Runner is the entrypoint for running a Cairo program and generating the AIR inputs needed for proof.
When a Cairo program is executed by the CairoVM, we could view the memory model as a Write-Once one.
Recap - Differences between the two Cairo machines
We could recap in a table the key differences between the deterministic Cairo machine, and the non-deterministic one.
| Deterministic Cairo Machine | Non-Deterministic Cairo Machine | |
|---|---|---|
| Usage | Prover | Verifier |
| Hints | Executed | Not aware of them |
| Memory | Complete memory | Public memory only |
| Trace | Full execution trace | Initial & Final states only |
Cairo Virtual Machine Architecture Diagram
The following diagram represent the architecture of the CairoVM, to generate the AIR inputs for the proof system.